After we parse the document's text using computer vision, we need a way of finding the names of any vaccines or shot types in the text. For Karp-Rabin to scan efficiently, we need a fast way to tell which shot type is present in a given text fragment.

From the 251

Our system indexes shot types using the CVX (vaccine administered) code set from the HL7 v2.5.1 standard. The CDC assigns unique CVX codes for 254 distinct vaccines currently or previously available in the United States. Separate entries are included for various combination shots, dosages, and delivery methods that define distinct products. Around half of the codes are assigned to inactive vaccines, and 40 codes are assigned to various iterations of the COVID-19 vaccine.

These shot types may include combination shots that confer immunity to several diseases in one shot. Combination shots are typically named using portmanteaus of their constituent vaccines. For example, DTaP-Hep B-IPV is a single dose that combines the DTaP, Hepatitis B, and IPV (polio) vaccines. We need a way to tell the difference between a standalone Hep B vaccine and one administered as part of a combination DTaP-Hep B-IPV shot.

Karp-Rabin is helpful here, taking our shot types as the patterns to detect in the input document. For the algorithm to work, we need to construct a hash function that can quickly indicate an approximate match between a partial subsequence of text and a complete shot type in our recognized dictionary.

Hay is for hashes

Before we do some computer science, let’s clarify our goals. Our hash function must be:

• precise enough to distinguish similar shot types, like MMR and MMRV

• accurate enough to correct a typo or partial match like MNR

We satisfy these requirements using a two-tier approach of text matching against our corpus of known shot types.

Dice’s coefficient

The most common kind of typos are single-character substitutions. It's tempting to count the number of characters that match a shot type and the candidate text. If there's enough overlap, we've probably found a match.

Quickly we run into problems. "MMR" has three characters in common with both shot types MMRV and MMR. The latter MMR is the obvious choice. We must tweak the calculation to prioritize these complete matches, normalizing over length. Before too long, we wind up calculating Dice's coefficient.

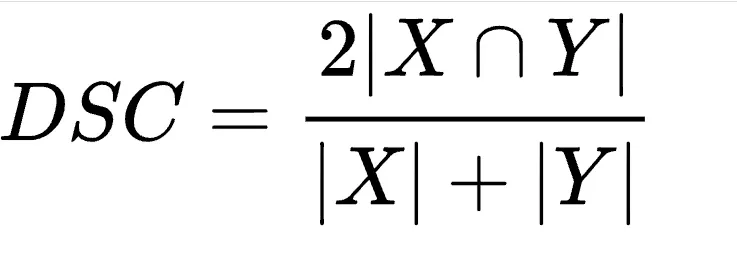
The numerator represents twice the number of elements shared between the sets X and Y. The denominator represents the total number of elements between X and Y

Dice's coefficient is a statistical measure of the similarity of two samples. This calculates the size of the overlap between the samples, adjusting for differences in size. When our samples are two pieces of text, Dice's coefficient will indicate how similar the two pieces appear.

Insertions or deletions into the candidate text will shift letters back and forth. We won't be able to match texts using only the position of the letters. Instead, we calculate the set of bigrams in each text. Each bigram represents a two-character subsequence within the complete text.

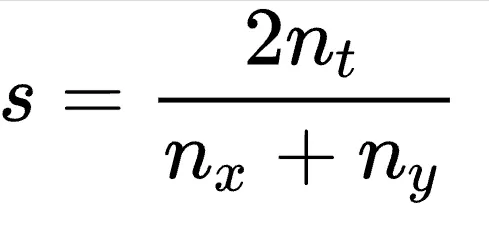
The numerator represents twice the number of bigrams shared between the two texts. The denominator is the total number of bigrams between the two texts.

For a candidate text "MMR," our bigrams are MM and MR. Our shot type MMRV has the bigrams MM, MR, and RV. They share two bigrams, MM and MR.

We calculate Dice's coefficient by doubling the shared bigrams between the texts. Then, we divide by the total number of bigrams across the two texts.

s = 2(2) / (2 + 3) = 0.8

In this case, Dice's coefficient between "MMR" and MMRV is only 0.8. This is lower than the perfect match MMR of 1.0. The system will correctly label the token as MMR.

Levenshtein distance

Our calculation of Dice’s coefficients sometimes fails to indicate a matching label for the candidate text. Often, there are several credible matches for a candidate text. In both cases, we use another text similarity measure as a fallback or tie-breaker.

Levenshtein distance quantifies the difference between two chunks of text. It measures edit distance or the number of characters that must change to transform one text to another. Levenshtein distance thus accounts for insertions, deletions, and simple point substitution of single characters. This metric is especially useful for correcting typos and handling variations like truncation.

Unlike Dice’s coefficient, the calculation doesn’t depend on the presence of specific pairs in the sequence. The presence or absence of each character in the pattern and candidate texts factors into the result match independently. This makes Levenshtein distance resilient to both typos and overlapping patterns.

Although this approach is exacting, it’s also very inefficient. The algorithm has a runtime of O(n^2), where n is the length of the texts or patterns in question. If we calculated the Levenshtein distance between every term in the candidate text and each entry in our dictionary of shot types, processing the document fully would take a long time. Instead, we use this more sensitive definition of string similarity only when Dice’s coefficient fails to indicate a clear match.

How did we do?

Using this hybrid approach, we keep the overall expected runtime of our new hash function much closer to the O(n) achieved by the first prong of our test. Thanks to the added sensitivity by the second prong, we still achieved high accuracy. In the field, we typically identify most shot types correctly in a given immunization record on the first try.

To further tune performance, we’ve introduced an additional layer of synonyms representing the myriad ways each shot type may be represented in text across documents from different states. In most cases, appropriately discriminative synonyms are enough to disambiguate any unmatched shot types left over after processing. This allows our research and operations teams to refine our system even closer to 100% accuracy.